為什麼要學時間與空間複雜度？

在寫程式時，除了讓程式正確運作，還要考慮執行速度和記憶體使用量。
這就是時間複雜度（Time Complexity和 空間複雜度（Space Complexity）的概念。

  • 時間複雜度的意義
    當資料量很小時，任何演算法看起來都可能表現得很好。
    但當輸入 n 變大（例如上百萬筆數據）時，使用到不好的演算法會非常慢很沒有效率。

    範例：
    搜尋一個數字
    暴力搜尋（O(n)）：每次都從頭找，資料量大時超慢。
    二分搜尋（O(log n)）：資料有排序時，搜尋超快。

  • 空間複雜度的意義
    有些演算法為了快，會多開陣列來存資料（佔空間）。
    有些則是盡量用少量記憶體，但可能會比較慢。

    範例：
    開一個新陣列來存排序結果（O(n) 空間）
    直接在原陣列排序，不開新陣列（O(1) 空間）

時間 vs. 空間的權衡

有些演算法速度快，但需要更多記憶體，有些則相反。
例如：

  • 用 Hash Table（字典）加速搜尋，會用更多記憶體
  • 不用陣列、直接在原資料上排序（In-Place Sorting），會比較慢，但省記憶體
  • 遞迴函式可能很慢，還會佔用大量記憶體堆疊

什麼是時間複雜度(Time Complexity)

時間複雜度：
即演算法的執行時間如何隨輸入大小變化，通常用 Big O notation 來表示。

常見的時間複雜度

時間複雜度 名稱 範例
O(1) 常數時間 直接存取 arr[0]
O(log n) 對數時間 二分搜尋
O(n) 線性時間 遍歷陣列
O(n log n) 準線性時間 快速排序
O(n²) 平方時間 巢狀迴圈
O(2ⁿ) 指數時間 遞迴解費氏數列
O(n!) 階乘時間 排列組合問題

什麼是空間複雜度（Space Complexity）

空間複雜度
即演算法運行時需要的額外記憶體。

常見空間複雜度

符號 名稱 例子
O(1) 常數空間 只用幾個變數
O(n) 線性空間 用一個陣列來存結果
O(n²) 平方空間 二維矩陣

Big O notation

Big O ：

用來描述演算法執行時間或記憶體使用量隨輸入大小（n）變化，評價演算法好壞的一種基準。

  • 只看最壞情況
  • 忽略常數與低階項

Big O 評價：
O(1)最好 O(n!)最差，如下方圖片所示：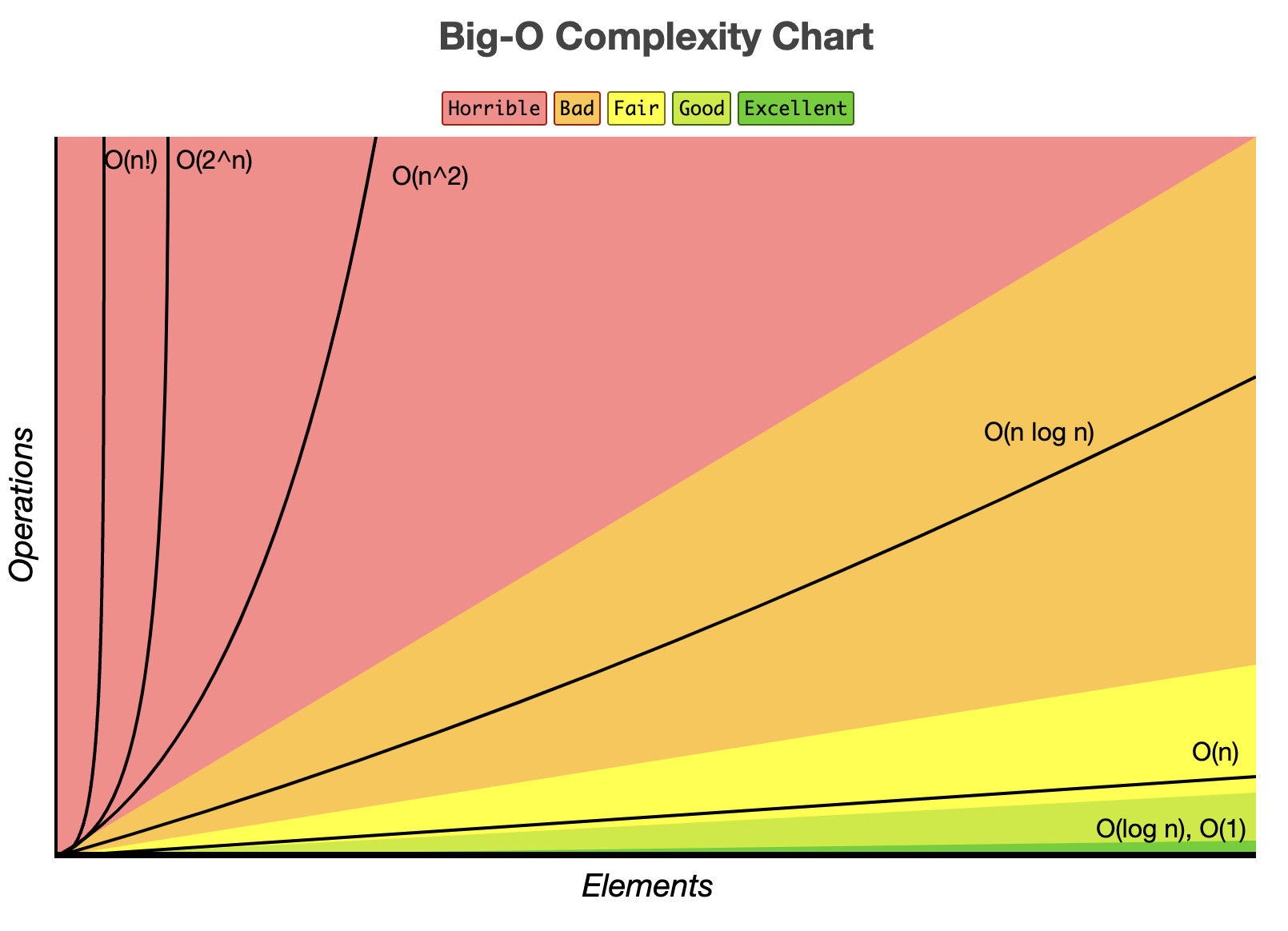
排名

參考來源

總結

時間複雜度（Time Complexity） 決定程式跑多快
空間複雜度（Space Complexity） 決定程式吃多少記憶體
時間複雜度好的情況，可能會比較佔空間
空間複雜度好的情況，可能會比較慢